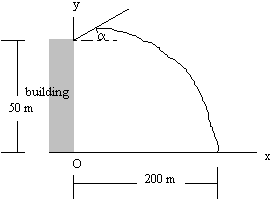
Question 1:
(a) Evaluate (i) 
(ii) 
using the subst. u = 1 + 5x.
(b) The polynomial 
has a factor (x + 3). Find the value of a.
(c) The point P(-3, 8) divides the interval AB externally in the ratio k:1 . If A is the point (6,-4), find the value of k.
(d) (i) Sketch the graph of y = |x - 2|
(ii) For what values of x is |x - 2| < x ?
Question 2:
(a) Consider 
wher k is a constant.
(i) Find 
and 
(ii) Determine the values of k for which satisfies the equation 
(b) When Mendel crosses a tall strain of pea with a dwarf strain of pea, he found that 3/4 of the offspring were tall and 1/4 were dwarf.
Suppose that five such offspring were selected at random. Find the probability that
(i) all of these offspring were tall;
(ii) at least three of these offspring were tall.
(c) The diagram shows two circles intersecting at A and B. The diameter of one circle is AC. Copy this diagram into your booklet.
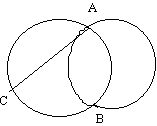
(i) On your diagram draw a straightline through A, parallel to CB, to meet the second circle in D.
(ii) Prove that BD is a diameter of the second circle
(iii) Suppose that BD is parallel to CA. Prove that the circles have equal radii.
Question 3:
(a) Taking x=0.5 as a first approximation to the root of the equation 
, use Newton's method to find a second approximation.
(b) Evaluate 
(c) If 
, find dy/dx when x = 1.
(d) The volume V of a sphere of radius r mm is increasing at a constant rate of 200 mm3 per second
(i) Find 
in terms of r.
(ii) Determine the rate of increase of the surface area S of the sphere when the radius is 50 mm (note: 
)
Question 4:
(a) Use mathematical induction to prove that, for all positive integers n,
1 + 2 + 4 + . . . . . + 
(b) The acceleration of a particle moving in a straight line is given by 
, where x is the displacement in metres from the origin O and t is the time in seconds. Initially, the particle is at rest at x=4.
(i) If the velocity of the particle is v m/s show that 
.
(ii) Show that the particle does not pass through the origin.
(iii) Determine the position of the particle when v=10.
(c) Containers are coded by different arrangements of coloured dots in a row, the colour are white and at most one is blue.
(i) Find the number of different codes possible if six dots are used.
(ii) On some containers only 5 dots are used. Find the number of different codes possible in this case.
Question 5:
(a) Consider the function 
(i) Evaluate f(2)
(ii) Draw a graph of y = f(x)
(iii) State the domain and range of y = f(x).
(b) (i) Sketch the parabola whose parametric equations are x = t and y = t2. On your diagram mark the points P and Q which correspond to t = -1 and t=2, respectively.
(ii) Show that the tangents to the parabola at P and Q intersect at R(1/2, -2).
(iii) Let T(t, t2) be the point on the parabola between P and Q such that the tangent at T meets QR at the midpoint of QR. Show that the tangent at T is parallel to PQ.
Question 6:
(a) (i) On the same axes, sketch the curve y = sin x , y= cos x, and y = sinx + cos x, for 0<x<2
, show that the x- and y- component of displacement are 
.