I. INTRODUCTORY PROBLEMS
1. Solve the following quadratic equations with complex roots:
(a) 
(b) 
(c) 
(d) 
(e) 
2. If 
, express as a complex number in the form x + iy:
(a) 
(b) 
(c) 
(d) 
(e) 
(f) 
(g) 
(h) 
3. If 
and 
, find in the form x + iy the following:
(a) 
(b) 
(c) 
(d) 
4. Find real number x and y such that:
(a) 
(b) 
(c) 
5. Find z in the form z = x + iy
(a) 
(b) 
6. Find the linear factor of :
(a) 
(b) 
(c) 
(d) 
(e) 
(f) 
(g) 
(h) 
7. Show that for 
where 
that
(a) 
(b) 
(c) 
(d) 
(e) 
(f) 
(g) 
(h)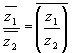 
(i) 
is a real number. (j) 
is an imaginary number.
(k) 
is a real number.
8. (i) Show that
= 
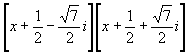
(ii) Similarly find the complex factors of
(a) 
(b) 
(c) 
(d) 
(e) 
(f) 
9. Note that 
, prove that the solutions of 
are :
. These solutions are called the cubic root of unity, since they are the roots of . The solutions 
are called the complex cubic roots of unity, whilst x=1 is called the real cubic root of unity. If these complex roots are denoted by 
and 
, verify that 
and
, a3 = b3 = 1, 1+a+b=0. [Note that in practice, we denote the roots of as 1 w2 and w3 = 1 , and 1+w+w2 = 0].
10. Simplify the following expressions:
(a) 
(b) 
(c) 
(d) 
(e) 
(f) 
(g) 
(h) 
(i) 
11. If 
and 
, find (a) 
(b)
(c) 
(d) 
.
12. Given that 
, express in the form of X + iY :
(a) 
(b) 
(c) 
(d) 
13. Solve for 
and 
in the following simultaneous equations:
and 
14. Let 
, prove that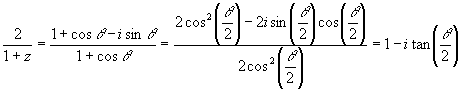 
15. If 
, find x and y when :
(a) 
(b) 
16. (i) If 
, express x and y in terms of a and b.
(ii) If 
, where , express u and v in terms of x and y.
(iii) If 
, where a,b,c,d,x,y are real, x and y in terms of a,b,c,d.
(iv) If 
, Find the real numbers A, B, C, D.
17. If 
, where x, y, a, b are real and a>0, prove that 
and 
.Hence express 
in the form of .
18. (i) Prove that 
(ii) Find x in the domain 
, if 
.
20. Divide 
by 
, and hence prove that the 3 cube roots of 
are 
and 
.