1. If m = 2, n = 3 and p = 4, evaluate the following:

(a) (b) (c) (d) (e)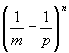

2. Simplify the following expressions:

(a) (b) (c)

(d) (e) (f) (g)

3. Simplify: (a) (b)

4. Let , (a) find f when v = 20, u = 25 (b) find v when f = 20 and u = 25.

5. Factorise:

(a) (b) (c) (d)

6. Simplify the following expressions:

(a) (b) (c)

(d) (e) (f)

7. Solve the following equations:

(a) (b) (c)

(d) (e) (f)

8. Luke works for a mining company at a wage rate of $12.80 an hour. If he works underground he is paid an extra rate of $3.65 per hour. Find his weeky wage if during the normal 40 hours, he works underground for 6 hours.

9. Change the following equation for an indicated subject:

(a) , [b] (b) , [h] (c) , [a]

(d) [ r] (e) , [x] (f) , [d]

10. Rationalise the following denominator and simplify:

(a) (b) (c)

11. Solve the following simultaneous equations:

(a) (b)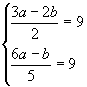

12. A father is 7 times as old as his daughter. In 5 years time he will be 4 times as old as his daughter will be then. How old each one now?

13. Solve the following quadratic equations by "complete-the-square" technique:

(a) (b) (c)

14. Show that the equation is parallel to the line joining the points (-1, 5) and (1, 9).

15. AB is a line which passes through (2, 3). What is the equation of AB if it is perpendicular to the line y = 5x + 2.

16. Find the equation of the locus of a point P(x, y) which moves so that its distance from the point (-2, 1) is equal from the line y = -1. Express the locus in the from and hence show that it is a parabola.

17. The parabola passes through the points (-2, 18) and (1, 3). Find the values of a and b.

18. Show that the line y = x - 4 is a tangent to the circle , and find the coordinates of the point of contact.

19. Without solving the following equations, determine whether they have two roots, one root or no solution:

(a) (b) (c) (d)

20. Find the sum of all numbers between 20 and 200 that are divisible by 5.

21. Find the sum of all numbers between 20 and 200 that are NOT divisible by 5.

22. If and are two consecutive terms of a GP series, find, in surd form, the next term and the sum to infinity.

23. Prove that

(a) (b)

24. Solve the following trigonometric equations:

(a) (b)

25. Solve the following inequalities:

(a) (b) (c) (d)