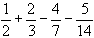
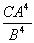 where
where 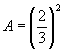 ;
; 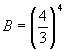 ;
; 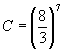
The Vietnamese Mathematical Hobby Group
MATHEMATICAL TEST PAPER #7
Question 1:
(i) Find the exact value (as a rational number in its lowest terms) of:
(ii) If the volume of one litre of a certain liquid decreases to V litres after n days according to the formula ![]() , find the value of r (to 3 significant figures) if V = 0.31 after 5 days.
, find the value of r (to 3 significant figures) if V = 0.31 after 5 days.
(iii) In the triangle ABC the side BC has length 4 cm, and the angles at B and C are 60o, 70o, respectively. Determine
(a) the length of AB.
(b) the length of AP where P is the midpoint of BC.
Question 2:
(i) Differentiate with respect to x (a) ![]() (b)
(b) ![]()
(ii) Write down the primitives of (a) sin 2x (b) ![]() (c)
(c) ![]()
(iii) Express sin 40o![]() cos 25o in the form of
cos 25o in the form of ![]()
(iv) Evaluate (a) ![]() (b)
(b) ![]()
Question 3:
(i) For what value of the constant B are the graphs of the linear equations: x - 4y + 4 = 0 and 2x + By - 2 = 0, are (a) parallel (b) perpendicular ?
(ii) Indicate, using a sketch the region of the cartesian plane for which the following inequalities hold simultaneously: x - 4y < -4 = 0 and 4x + y < +4.
(iii) Sketch the graph of ![]()
Question 4:
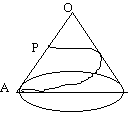
A thin sheet of smooth metal is in the shape of a sector of a circle with OA, OB as bounding radii each of length 10 cm, and the angle AOB is 60o.
(i) Find the length of the arc AB and the area of the sector.
(ii) The sheet is now bent to form a right circular cone by welding the bounding radii OA, OB together (and inserting a circular disc to close in the cone at the base).
(a) Find the volume of the cone. (Note: the volume of a right circular cone is ![]() )
)
(b) On the surface of this cone a thin string is pulled tight starting with one end fixed at the point A and once round the cone to the other end P which is at the midpoint of OA (as illustrated in the diagram). Find the length of this string.
Question 5:
(i) For the sequence 2, -1.5, . . . . write down the expressions for the nth term and the sum to n terms for two cases:
(a) the sequence is arithmetic (b) the sequence is geometric
Evaluate each of these four expressions when n = 4 and, in these cases where it exists, the limit as ![]()
(ii) Write down the formula for the sum of the first n positive odd integers. Explain the method of mathematical induction and use it to prove this formula.
Question 6:
(i) For the curve y = f(x) it is given that f'(x) = 4x - 2 and the curve passes through the point (1, 0). Deduce the equation of this curve and show that it also passes through the origin.
(ii) Show that this curve is parabola; find its focal length, the coordinates of its focus and the equation of its directrix.
(iii) Sketch the region in the cartesian plane bounded by this parabola, its tangent at (1,0) and the line x = 0. Find the equation of this tangent and hence calculate the area of the region.
Question 7:
(i) Find the minimum and maximum values of ![]()
Question 8:
(i) Two cars, represented by point A and B, are travelling due East and due North, respectively along two roads represented by two straightlines intersecting at O. At a certain instant, car A is 2 km west of O and car B is 1 km south of O, the former travelling at a constant speed of 1 km/minute and the latter at constant speed of V km/minute.
(a) What value of V will cause a collision ?
(b) Prove that, in the course of motion, the minimum distance between the cars is ![]() .
.
(ii) Determine the range of values of V which will cause collision in the above if the problem is made more realistic by representing the cars, not by point A and B, but by rectangles each of length a km and width b km, with their centres at A and B.
Question 9:
(i) (a) Write down the value of ![]()
(b) By comparing the coefficients of ![]() on both sides of the identity
on both sides of the identity ![]() , show that
, show that ![]()
(ii) A tosses a coin 16 times, what is the probability that it falls heads uppermost on 8 occasions ?
(iii) A tosses a coin 8 times and, quite independently, B also tosses a coin 8 times. Find the probability:
(a) the number of heads obtained by A equals the number of heads obtained by B.
(b) the number of heads obtained by A plus the number obtained by B is 8.
(iv) Describe experiements similar to those in (ii) and (iii) which would lead to the conclusion ![]()
Question 10:
(i) Calculate the volume of the solid generated when the region in the first quadrant bounded by the curve ![]() , the line
, the line ![]() and the coordinate axes, is rotated about the x-axis.
and the coordinate axes, is rotated about the x-axis.
(ii) The motion of a pendulum may be approximately represented by the equation ![]() , where x is the displacement at time t. Th con stants g and L represent the value of gravity at the earth's surface and the length of the pendulum respectively. Consider the case
, where x is the displacement at time t. Th con stants g and L represent the value of gravity at the earth's surface and the length of the pendulum respectively. Consider the case ![]() .
.
(a) Let ![]() , show that
, show that ![]()
(b) The pendulum is swinging in accordance with the initial condition t = 0 , x = 0, and v = p.
Using the approximate equation of motion above to find the first value of x where v=0.
(c) The motion of the pendulum may more accurately be represented by ![]() .
.