(i) Integrate the following functions by using the given substitution

(ii) Show that the equation  has a root near x = 1. Trying to improve this root by the Newton's method will fail; explain why ?

(iii) If , prove that  and hence show that y increases as x increases in the domain .

(iv) By giving x an appropriate value in  prove that

(a)  (b) 

[ans: (i) (a)  (b) ]

Question 2

(i) Use the substitution  to show that 

(ii) Factorise the polynomial , given that P(x) has a repeated root.

(iii) The polynomial Qx) has the form Qx) = P(x) (x+a) with P(x) as in (ii) and where the constant a is chosen so that Q(x) > 0 for all real x. Find possible values of a.

(iv) A particle undergoes a SHM about the origin O. Its displacement x from O is given by  where t is the time (in seconds).

(a) Express the acceleration as a function of displacement

(b) write down the amplitude

(c) find x for which the speed is maximum and this speed.

Question 3

(i) A meeting room contains a round table with 10 chairs. These chairs are equally spaced and indistinguishable.

(a) A committee of 10 persons included 3 teenagers are to seat. How many sitting arrangements can be done if the teenagers are to sit together ?

(b) Elections are held for the position of chairperson and secretary in a 2nd committee of 10 people seated around the table. What is the probability that the 2 elected people are sitting directly opposite each other ?

(ii) A scientist found that the amount Q(t) of a substance present in a mineral at time t is satisfied the equation 

(a) verify that Q(t) =  satisfied this equation for any constant A>0.

(b) If Q(0) = 10 mg, find the maximum value of Q(t) and the time at which this occurs.

(c) Describe what happen to Q(t) when t increases indefinitely.

Question 4

(i) If  prove that .

(ii) A sequence (known as the Fibonacci sequence) is defined as  (n > 2). Prove by mathematical induction that

(iii) If . Express  in terms of y. Hence solve the equation .

Question 5

(i) In a certain GP series, the sum of the first 4 terms is -5 and the sum of the first 8 terms is . Show that  and that . Hence by division, show that  and that r = +1/2. Show that there are two possible sequences and find them.

(ii) By considering a right angled triangle in which the hypotenuse is 1 unit and the other sides is x units. Show that for 0<x<1, 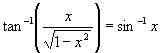. Furthermore, prove by substitution that 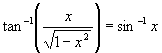 for (a) x = 0 (b) 1<x<0.

(iii) Hence verify the result for the derivative of 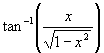 obtained in (ii).

Question 6

(i) Prove that 

(ii) P and Q are points on a circle and the tangents to the circle at P and Q meets at S. R is a pont on the circle so that PR // QS. Prove that PQ = QR.

(iii) A circle has equation 

(a) Find the centre and radius of the circle.

(b) The line x + 2y = 0 meets the circle at A and B. Find the coordinates of A and B and hence its length.

Question 7

(i) A wall 27 m high stands on a horizontal plane. From a point O in this plane, a ball is projected in a plane at right angles to the wall at an angle  with the horizontal, where tan = 3/4. The ball just clears the top of the wall. If O is 96 m from the wall, find the time taken to reach the wall and show that the speed of projection is 40 m/s.

(a) Find the greatest height to which the ball will rise beyond the horizontal plane.

(b) Find the range.

(ii) The chord PQ in the parabola  subtends a right angle at the vertex of the parabola. The normals to P and Q meets at R.

(a) Prove that pq = -4 where p and q are parameters of the points P and Q.

(b) Show that as P and Q take varied positions on the parabola, the locus of R is .