1. Solve the inequality .

2. Find the exact value of .

3. Evaluate by using the substitution u = 2t - 1.

4. If y = cos(lnx), find: (a) (b)

5. A class consists of 10 girls and 12 boys. How many ways are there of selecting a committee of 3 girls and 2 boys from this class ?

6. Prove that:

7. (a) On the same diagram, sketch the graph of and y = |2x - 1|.

(b) By using (a) or otherwise, determine the value of c the equation has exactly two solutions.

8. Suppose that the cubic has a relative maximum at and a relative minimum at .

(a) Prove that .

(b) Deduce that the point of inflexion occurs at .

9. Consider the function .

(a) Evaluate f(0)

(b) Draw the graph of y = f(x)

(c) State the domain and range of y = f(x).

10. When the polynomial P(x) is divided by , the remainder is 3x - 1. What is the remainder when P(x) is divided by x- 1.

11. The velocity v m/s of a particle moving in simple harmonic motion along the x-axis is given by: .

(a) Between which two points is the particle oscillating?

(b) What is the magnitude of the motion?

(c) Find the acceleration of the particle in terms of x

(d) Find the period of the oscillation.

12. In the following diagram, AB is the diameter of the circle centre O, and BC is tangential to the circle at B. The line AED intersects the circle at E and BC at D. The tangent to the circle at E intersects BC at F. Let EBF = .

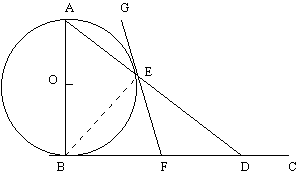
(a) Copy the diagram into your bokklet and mark all information given.

(b) Prove that FED =

(c) Prove that BF = FD.

13. Five travellers arrive in a town where there are 5 hotels.

(a) How many different accommodation arrangements are there if there are no restriction on where the travellers stay?

(b) How many different accommodation arrangements are there if each traveller stays at a different hotels?

(c) Suppose two of the travellers are husband and wife and must go to the same hotel. How many different accommodation arrangements are there if the other three can go to any of the other hotels?

14. (a) Sketch the graph of y = cosx for 0 < x < 2p.

(b) By using (a) or otherwise, find those values of x satisfying 0 < x < 2p for which the gometric series 1 + 2cosx + 4cos2x + 8cos3x + . . . . has a limiting sum.

15. For n = 1, 2, 3, . . ., let .

(a) Use math induction to prove that for n = 1, 2, 3, . . .,

(b) By using the result of (a) estimate the least value of n such that .

16. (a) Prove that the graph of y = lnx is concave down for all x > 0.

(b) Sketch the graph of y = lnx.

(c) Suppose that 0 < a < b, and consider the points A(a, lna) and B(b, lnb) on the graph of y = lnx. Find the coordinates of the point P that divides the line segment AB in the ratio 2:1.

(d) By using (a) and (b) deduce that .

17. Consider the following graph of y = f(x). The value a shown on the axis is taken as the first approximation to the solution b of f(x) = 0.

Is the second approximation obtained by Newton's method a better approximation to b than a is ? Give a reason for your answer.

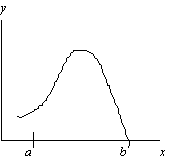
18. Let T be the temperature inside a room at time t and let A be the constant outside air temperature. Newton's law of cooling states that the rate of change of the temperature T is proportional to (T - A).

(a) Show that , where C and k are constant, satisfies the statement.

(b) The outside air temperature is 5oC and a heating system breakdown causes the inside room temperature to drop from 20oC to 17oC in half an hour. After how many hours is the inside temperature equal to 10oC ?

19. In the following diagram, the x-axis represents a major blood vessel, whilst the line PA represents a minor blood vesssel that joins the major blood vessel at P. The point A has cooridinates (l, d) and PA makes an angle with the normal to the x-axis at P, as shown in the diagram.

It is known that the resistance to flow in a blood vessel is proportional to its length, where the constant of proportionality depends upon the particular blood vessel.

Let R be the sum of the resistances to flows in OP and PA.

(a) Show that

(b) The blood vessel PA is joined to the blood vessel Ox uin such a way that R is minimised. If , find the angle q that minimises R (You may assume that l is large compared to d).

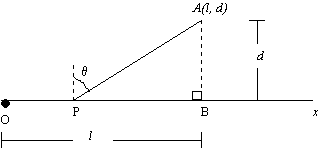
20. Consider the parabola wher a>0, and suppose that the tangents at and intersect at the point T. Let S(0, a) be the focus.

(a) Find the coordinates of T.

(b) Show that SP =

(c) Suppose that P and Q move on the parabola in such a way that SP + SQ = 4a. Show that T is constrained to move on a parabola.

21. (a) A projectile is fired from the origin O with velocity V and with angle of elevation , where . Show that the x and y displacements are:

and

(b) Show that the equation of flight of the projectile can be written as: where .

(c) Show that the point (X, Y), where , can be hit by firing at two different angles and , provided that .

(d) Show that no point above the x-axis can be hit by firing at two different angles and , satisfying and .