1. Differentiate (a) xcosx (b)

2. Find the coordinates of the point P which divides the interval AB with ends A(2, 3) and B(5, -7) internally in the ratio 4:9

3. Evaluate (i) (b)

4. Find the number of six-letter arrangements that can be made from the letters word SYDNEY.

5. (a) Draw a sketch of . State the domain and range.

(b) A region bounded by the curve , the x-axis and the line x = 1. Use Simpson's rule with three function values to find an approximation of the area of R. Give your answer correct to 2 dp.

6. Find by using the substitution u = .

7. If a, b and g are the roots of the equation . Find

(a) a + b + g (b) abg (c) 1/a + 1/b + 1/g

8. A particle undergoes simple harmonic motion about the origin O. Its displacement x m from O at time t seconds, is given by: .

(a) Express the acceleration as a function of displacement.

(b) Write down the amplitude of the motion.

(c) Find the value of x for which the speed is maximum and determine this speed.

9. Prove by math induction that for n > 1:

10. Given that 0 < x < p/4, prove that

11.

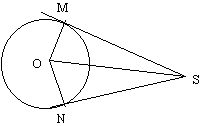
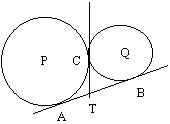
(a) SM and SN are tangents drawn from an external points S to a circle with centre O. The points of contact of these tangents with teh circle are M and N. Prove that SM = SN.

(b) Two cicles touch externally at C. The circles which have centresP and O, are touched by a common tangent A and B respectively. The common tangent at C meets AB at T. Show that AT = TB and that ACB is a right triangle.

12. (a) Divide the polynomial by .

(b) Write , where q(x) and r(x) are polynomials and r(x) has degree less than 2.

(c) Hence show that and have no zeros in common.

13. (a) Find the stationary points for the curve for 0<x<2p. Determine whether they are relative minima or maxima.

(b) Find the coordinates of those points on the curve corresponding to x = 0, p and 2p.

14. A meeting room contains a round table surrounded by 10 chairs. These chairs are indistinguishable and equally spaced around the table.

(a) A committee of 10 people includes 3 teenagers. How many seating arrangements are there in which all three sit together?

(b) Elections are held for the positions of Chairperson and Secretary in a second committee of 10 people seated around this table. What is the probability that the two people elected are sitting directly opposite each other.

In both answers you must write a brief reasoning.

15. (a) Show that the equation of the tangent to the parabola at any point is given by .

(b) S is the focus of the parabola and T is the point of intersection of the tangent and the y-axis. Prove that SP = ST.

(c) Hence show that SPT is equal to the acute angle between the tangent and the line through P parallel to the exis of the parabola.

16. Suppose that

(a) Use the Binomial theorem to write an expression for where k = 0, 1, 2, . . . , 25.

(b) Show that .

(c) Hence or otherwise find the largest coefficient . You may leave your answer in .

17. Water is poured into a conical vessel at a constant rate of 24 cm3 per second. The depth of water is h cm at any time t seconds. What is the rate of increase of the area of the surface S os the liquid when the depth is 16 cm.

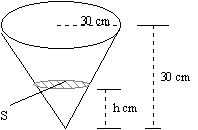
18. A parcel in the shape of a rectangle prism has sides x cm, x cm and y cm. The girth is the smallest distance around the parcel. A courier Company will diliver parcels for which the largest side L cm and the girth g cm satisfy L + g < 100.

Find the dimensions of the parcel of the largest volume, for which L + g = 100, that the Courier Company will deliver.