6. Find the equation of the curve given that the gradient at any point P(x, y) is 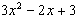 and that the point (3,3) belongs to the curve.
and that the point (3,3) belongs to the curve.
7. For the function 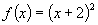 find the rule that defines the function F, where F'(x) = f(x) and F(1) = 4.
find the rule that defines the function F, where F'(x) = f(x) and F(1) = 4.
8. Find the equation of a curve given that 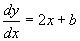 at any point P and that when x=3,
at any point P and that when x=3, 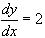 and y = -3.
and y = -3.
9. Find the rule that defines a function f, given that f'(x) = 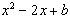 for all x, and f'(0) = 1 and f(0) = 2.
for all x, and f'(0) = 1 and f(0) = 2.
10. A curve contains the point (0,4) and its gradient is (x-1)(x+2) at any point on the curve. Find the equation of the curve.
11. At all points on a certain curve 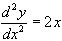 . The point (3,6) belongs to the curve and its tangent at this point is inclined at 45o to the X-axis. Find the equation of the curve.
. The point (3,6) belongs to the curve and its tangent at this point is inclined at 45o to the X-axis. Find the equation of the curve.
12. Find the primitives of
(a) 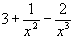 (b)
(b) 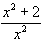 (c)
(c) 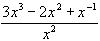 (d)
(d) 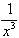 .
.
13. In each of the following, find f(x) given that:
(a) 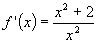 (b)
(b) 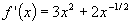
(c) 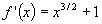 (d)
(d) 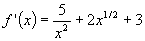
14. Given that 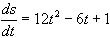 , find s in terms of t given that s=4 when t=1.
, find s in terms of t given that s=4 when t=1.
15. Given that 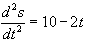 , t>0 and
, t>0 and 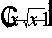 and s=0 when t=0, find
and s=0 when t=0, find
(a) t when 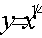 (b) s when
(b) s when 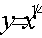 .
.
[ans: (a) 12 (b) 432]
16. Given 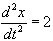 for all t > 0 and
for all t > 0 and 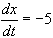 and x = 4 when t = 0, find t when
and x = 4 when t = 0, find t when
(a) 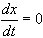 (b) x = 0.
(b) x = 0.
[ans: (a) 5/2 (b) 1 or 4]
![]() (ii)
(ii) ![]()
![]() (iv)
(iv) ![]()
![]() (vi)
(vi) ![]()
![]() (viii)
(viii) ![]()
![]()
![]() (b)
(b) ![]()
![]() (d)
(d) ![]()
![]() (f)
(f) ![]()
![]()
![]() ]
]