Integrating the following with respect to x
1. ![]() 2.
2. ![]() 3.
3.![]()
4. ![]() 5.
5. ![]() 6.
6. ![]()
7. ![]() 8.
8. ![]() 9.
9. 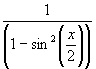
10. ![]() 11.
11. 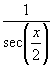 12.
12. ![]()
13. ![]() 14.
14. ![]() 15.
15. ![]()
16. ![]() 17.
17. ![]()
Find the following integrals:
18. ![]() 19.
19. ![]()
20. ![]() 21.
21. ![]()
22. ![]() 23.
23. ![]()
24. ![]() 25.
25.![]()
26.![]() 27.
27.![]()
28. ![]()
29. (a) Show that ![]() , and hence find
, and hence find ![]()
(b) Show that ![]() , and hence find
, and hence find ![]()
(c) Prove that ![]() , and hence find
, and hence find ![]()
(d) Prove by differentiation that ![]() =
= ![]() or
or
![]() . Show that each of the primitive functions differ only by a constant.
. Show that each of the primitive functions differ only by a constant.
30. Find the following integrals by using the substitution method:
(a) ![]() (b)
(b) ![]() (c)
(c) ![]()
(d) ![]() (e)
(e) ![]() (f)
(f) ![]()
(g) ![]() (h)
(h) ![]() (i)
(i) ![]()
(j) ![]() (k)
(k) ![]() (l)
(l) ![]()
(m) ![]() (n)
(n) ![]() (o)
(o)![]()
(p) ![]() (q)
(q)![]()
31. Determine the value of the following integrals:
(a) ![]() (b)
(b) ![]() (c)
(c)![]()
(d) ![]() (e)
(e)![]() (f)
(f) ![]()
(g)![]() (h)
(h) ![]()
32. (a) Find ![]() hence find
hence find![]() .
.
(b) Show that ![]() hence find
hence find![]()
(c) Show that ![]() hence find
hence find ![]()
(d) Differentiate ![]() and
and ![]() ; make use of these results to find
; make use of these results to find![]() .
.
(e) Show that ![]() and hence find
and hence find ![]() .
.
(f) Show that ![]() , and hence find
, and hence find ![]()
(g) Differentitate ![]() and hence find
and hence find ![]() .
.
33. (a) For what values of a does (i) ![]() and
and
(ii) ![]()
(b) Find (i) ![]() (ii)
(ii) ![]()
(c) Prove that (i) ![]() (ii)
(ii) ![]()
(iii) ![]() , hence find the following integrals:
, hence find the following integrals:
![]() ,
, ![]() ,
, ![]() .
.
(d) Show that (i) ![]()
(ii) ![]()
(iii) ![]()
(iv) ![]()