Use the factor theorem to show (1-4) that:

1. is a factor of

2. is a factor of

3. is a factor of

4. is a factor of

5. Given that , find the value of a if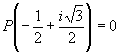

6. Given that , find the value of a if .

7. Given that , find the values of a and b if i and are zeros of P(x).

8. Given that , find the values of a and b if P(2)=0 and P(1-i)=0.

Complete factorise the following (9-24):

9. over C

10. over C

11. over (i) J (ii) C

12. over C.

13. over C.

14. over (i) J and (ii) C.

15. over (i) Q (ii) R (iii) C.

16. over (i) R (ii) C

17. over (i) R (ii) C.

18. over C.

19. over (i) R (ii) C.

20. over (i) R (ii) C.

21. over (i) R (ii) C given that is one linear factor.

22. over C.

23. over (i) R (ii) C.

24. over C.

Find z in (25-31);

25.

26. if (i) (ii)

27.

28.

29.

30.

31.

32. Find the values of the real numbers a and b , such that 1+i is a root of the equation

Find z in 33-39:

33.

34.

35.

36.

37.

38.

39.

Write down an equation of the lowest possible degree with (i) complex coefficients, (ii) rational coefficients and having the following among its roots:

40. 41. 42. ,

43. of multiplicity 2.

44. 45.

Find and ploton the complex plane (46-55):

46. The square root of 47. The square root of

48. 49.

50. 51. The cube root of 64.

52. The fourth root of 8. 53. The sixth root of -1

54. The sixth root of 64. 55. The cube root of -8.

56. Find real values of a for which ai is a solution of the polynomial equation

57. Find the values which the real numbers a and b must take for z=1 to be a root of the complex equation

58. If 1, , and are the cube roots of unity, prove that (i) , (ii) and (iii) .

59. If , prove that

(i)

(ii)

Show that the roots of are the four complex roots of . Deduce that

60. Find (a) the three roots of the equation

(b) the remainder when is divided by

61. Find the real numbers k such that is a root of the equation . Hence or otherwise find the three roots of the equation.

62. Solve the following equations using a calculus method.

(a) given that it has a root of multiplicity 2.

(b) given that it has a root of multiplicity 3.