1. By substituting an appropriate value for x, prove the following identities:

(a) (b)

(c) (d)

(e) (f)

(g) (h)

2. By considering the expansion of in ascending powers of x, prove the following identities:

(a) (b)

(c) and

(Hint: differentiate both sides of the expansion )

(d) and

(Hint: integrate both sides of the expansion )

3. If is the coefficient of in the expansion of , where n is a positive integer, show by differentiating the identity

(a) that

(b) that

(c) TWICE that

4. Write down the value of . By comparing the coefficients of on both sides of the identity , show that . (ans: value 0).

5. From the identity , by considering the coefficient of

(i) on both sides, show that

(ii) on both sides, prove that .

6. By equating the coefficient of xr on each side of the identities and , prove that and that .

7. By considering the coefficients of xn on both sides of the identity , prove that is equal to

(a) 0 if n is odd; (b) 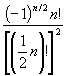if n is even.

8. (i) By considering the coefficient of on both sides of the identity , prove that

(ii) If and , and by considering the coefficients of in the product to obtain the value of (ans: )

(Hint: write the expansion of (1+x)n in reverse)

9. (i) By evaluating the integral in two different ways, prove the identity

(ii) Express in sigma notation. Then by eveluating the integral in two different ways, prove the identity where m = 2n+1. (ans: )

10. Find and hence evaluate

(i) Noting that and by using the binomial theorem to expand where n is a positive integer, prove that .

(ii) Use the above result to find the value (rational number) of the integral .

(ans: (ii) ).