1. Find the arithmetic and geometric means of the following:

(a) 4, 9 (b) -3, -27 (c) (d)

(e) (f) (g)

2. Find x if (i) x-1 is the geometric mean of (x-3) and (x+4).

(ii) 4x-1 is the arithmetic mean of (6x+2) and (x+12).

3. (i) Insert 5 arithmetic means between 15 and -21.

(ii) Insert 4 geometric means between 4/3 and -81/256.

(iii) Insert 29 arithmetic means between 5 and 50, and 3 geometric means between 7 and 112.

*4. Show that for a, b and c are positive.

5. Find the values of the following

(i) -3+5+13+ ...... to 15 terms (ii) to n terms.

(iii) (p-3q)+(3p-2q)+(5p-q)+..... to 21 terms.

(iv) to 8 terms.

6. Find the sum of the following:

(i) 9+5+1-3- ...... -387 (ii) log(8) + log(16) + log(32) + .....+ log(512)

(iii) (iv) -9+3-1+ ..... + 1/27

7. Find the values of the following:

(a) (b) (c)

(d) (e) (f)

8. (i) Show that if the sum of n terms of the series 15+13+11+.... is 55, then there are two possible values of n. Explain why this is true.

(ii) The sum of the n terms of the series 2+4+6+... is 420. Show that the values of n are both integral but that only one is valid.

9. Find n which gives the following sum.

(a) (b)

(c) (d)

10. Find the limiting sum or sum to infinity of the following:

(a) (b)

(c) (d)

(e) (f)

11. Evaluate the following sums

(a) (b) (c) (d)

12. By expressing each of the following recurring decimals as infinite series, find the value of each in simplest rational form.

(a) (b) (c) (d) (e) (f) .

13. In a certain AP series, the ratio of the sum of 10 terms to the sum of 5 terms is 13:4, and the sum of 20 terms is 115. If the series is a+((a+d)+(a+2d)+....., show that and hence that and that . Hence find a, d and the series.

14. In a GP series , the sum of the first 4 terms is -5 and the sum of the first 8 terms is ; show that and that , hence by division, show that and that . Show that there are two possible series and find each.

15. (i) The first and fourth terms of a GP sequence are 8 and -1, respectively. Find the sum of the first 7 terms.

(ii) The 5th and 11th terms of an AP sequence are -5 and -23, respectively. Find the 30th term and the sum of 30 terms.

16. (i) In the series , , . Show that there are two possible series and find in each case.

(ii) In the series , and , find .

17. (i) If is the sum of the first n terms of the series and if , find r.

(ii) If is the sum of the first n terms of the series a+(a+d)+(a+2d)+.... and if and , find the series.

(iii) If the last 3 terms of an AP of 21 terms add to 117, and the middle 3 terms add to 90, find the series.

18. (i) Find n if the sum of n terms of the series 2+5+8+.... is equal to the sum of the n terms of the series 47+45+43+...

(ii) For a certain GP, the third and sixth terms are -24, 3 respectively. Find the series and the sum of n terms (Sn). Also find the number of terms for which Sn differs from -64 by less than 0.001.

19. For what value of n is (a)

(b)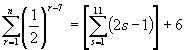

20. A farmer harvests 500 bushels of wheat in his first year on a farm. He harvested 550 bushels in the 2nd year and 605 bushels in the 3rd year. Each year, his harvest is 10% greater than the previous year. What does he harvest in his 10th year ? How much wheat can he sell altogether in his first 10 years.

21. An object falls through a distance of 16 m in the first second, 24 m in the 2nd second, 32 m in the 3rd second and in each succeeding second by 8 m further than the preceding second. How far does it fall in the eight second ? What is the total height through which it falls in 8 seconds ?

If this object was dropped from the Empire State Building 280 m above the ground, how long would it take to hit the ground.

22. The nth term of a series 25-5+5+..... is given by . Find the values of constants A and B, and thence obtain the 4th term of the series. Find the sum of this series (a) to n terms and (b) to infinity.