1. (i) Simplify (a) (b)

(ii) Solve for x: (a) (b)

(iii) Find x, y in: (a) AND

2. Find x if: (a) (b)

(c) (d)

3. (i) Simplify

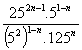(ii) Simplify (a) (b) (c)

4. (i) Show that and hence using factors prove that .

(ii) Uss factors to simplify: (a) (b) (c)

5. (i) Expand

(ii) If and , find the value of

6. Simplify (a) (b) (c) (d)

7. (i) If , express m in terms of n.

(ii) Simplify the following (without calculator)

(a) (b)

(iii) Solve for x: (a) (b)

8. (i) If , show that

(ii) Given , show that .

9. Find approximate solution of the following equations: (a) (b) .

10. (i) The sum to n terms of a certain series is . Using the formula , show that the nth term is .

(ii) Find the nth term and the first 3 terms of the series whose sum to n terms is .

11. The first two terms of an AP sequence are -29, -26. Write down the nth term (un) and the sum of the first n terms (Sn):

(i) What is the least value of n for which (a) and (b) .

(ii) The last term in this sequence is 46, find the number of terms and the sum of the terms of this sequence.

12. (i) If the last 3 terms of an AP sequence of 21 terms add to 117, and the middle 3 terms add to 90, find the progression.

(ii) The sum of the 2nd and 3rd terms of a GP sequence is 3, and the sum of the 4th and 5th terms is 12. Show that there are 2 possible sequences and find them.

13. For the sequence 7, 10, 13, ..... find

(i) f, the first term greater than 100;

(ii) l, the last term before 300;

(iii) n, the number of terms in this range (100 to 300).

14. For the sequence 3, -3/2 . . . . . write down expression for the nth term and the sum to n terms if the sequence is:

(a) arithmetic (b) geometric.

Evaluate each of these four expressions when n=6, and find the limit as n tends to infinity in those cases where it exists.

15. (i) Find the following sums: (a) -3 + 5 + 13 + . . . . . to 15 terms.

(b) to 9 terms.

(ii) Evaluate (a) (b)

(iii) Find the limiting sum of the following series:

(a) (b)

16. (i) Express (a) (b)

(ii) Find the sum to infinity of the GP sequence expressing your answer as a (a) surd with a rational number, and (b) decimal.

17. (i) The nth term of the series is . Find the values of A, B and the fourth term.

(ii) For a certain series , find the sum of the first n terms.

18. (i) Insert 44 arithmetic means between -3 and 87; find their sum.

(ii) Insert 8 geometric means between 512 and 1; find their sum.

19. (i) For a certain geometric series, the 2nd term is 6 and the sum to infinity is 49. Show that there are two possible values of r and find the corresponding series.

(ii) If , find the sum to infinity of the series , expressing the result in simplest form.

20. For the geometric series Show that if , then

Hence, find the least value of n for which () for the weries 6 + 3 + 1.5 + . . . . is less than 0.0001. {Hint: show that and then that Use calculator to find n).

21. Find the nth term of each of the following sequences:

(a) (b)

(Hint: In the nth terms, the numerator and denominator are the sums to n terms of a GP or an AP sequence).

22. A farmer harvests 500 bushels of wheat in his first year on a farm. He harvested 550 bushels in the 2nd year and 605 bushels in the 3rd year. Each year, his harvest is 10% greater than the previous year.

(a) What does he harvest in his 10th year ?

(b) How much wheat can he sell altogether in his first 10 years?

23. The grooves of a record can be assumed to be circular. There are 36 grooves to the cm, and on a particular record, the radii of the innermost and outermost circles are cm and cm. Find the number of grooves on the record, and calculate the total length (in metres) of the track on the record. (Take ) (hint: use )

24. For the GP , where

(note: this formula is useful when the number of terms is not easy to determine)

(i) Find the sum , and state whether this sum has a limit as (hint: use , where , and ).

(ii) Find the sum , and state whether this sum has a limit when ).

(iii) Determine the sum (where k is a fixed positive integer). Does this sum have a limit as .

25. The geometric series has a limiting sum S where , only if

-1 < r < 1 , i.e. if if .

Find the set of values of x for which the geometric series has a limiting sum, and determine this sum when it exists.

26. Find the sum to n terms of the series (a) 1 + 5 + 9 + . . . . . (b) 3 + 7 + 11 + . . . . .

Hence or otherwise, find the sum of the series 1 - 3 + 5 - 7 + 9 - 11 + . . . . to

(i) 100 terms , and (ii) to 101 terms.

27. (i) Find the sum as accurately as possible, by calculator.

(ii) A man invests $2000 at the beginning of each year in a fund which pays 10% p.a. interest on investments. Assuming the same rate of interest over the entire period, show that the value of his investment at the end of 20 years is

and hence find this ammount (to the neasrest $). {hints: if a sum $P is invested at r% p.a. compound interest for n years, then the amount $A to which this sum will accumulate is given by the formula }.