1. (i) Sketch the graph of 
. State the domain and range. Does y has a minimum value ? If so, is this a stationary value on the curve ?
(ii) For what values of x is 
defined ? Sketch the graph of y = , stating its range.
(iii) Define the function y = 
, and sketch it. Does y has a maximum value ? Explain your answer from the sketch.
2. Without using calculator, find the value of:
(a) 
(b) 
(c) 
(d) 
(e) 
(f) 
(g) 
(h) 
(i) 
3. Find the exact value of
(a) 
(b) 
(c) 
(d) 
4. Evaluate without tables:
(a) 
(b) 
(c) 
(d) 
(e) 
(f) 
5. Without tables, find the value of:
(a) 
(b) 
(c) 
(d) 
(e) 
(f) 
6. (i) Write down the result of sin(A + B) and hence deduce the result for 
. Use this to evaluate 
.
(ii) Write down a result for cos(x + y) and show that 
. Hence deduce the exact value of 
7. Determine the domain and range of each of the following functions:
(a) 
(b) 
(c) 
8. State the domain and range each of the following functions:
(a) 
(b) 
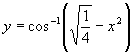(c) 
9. (i) Find the maximum value of the function 2x(1 - x) and hence determine the range of 
for 0 < x < 1.
(ii) Find the least value of x(x - 2) and hence determine the range of :
(a) 
(b) 
if for 0 < x < 2.
10. State the domain and range of cosx . Hence determine the domain and range of each of the following functions:
(a) 
(b) 
(c) 
(d) 
(e) 
(f) 
11. If n is a positive integer, determine the limits of the following sequences 
when:
(a) 
(b) 
(c) 
(d) 
(e) 
(f) 
12. Determine whether each of the following functions is an even or odd:
(a) y = sinx (b) 
(c) 
(d) 
(e) 
(f) 
(g) 
(h) 
(i) 
13. (i) Prove that 
is an odd function.
(ii) Provided -1 < x < 1 show that 
= x .
(iii) Hence, draw the graph of y = .
(iv) Using a similar method to show that
(a) 
for -1 < x < 1 (b) 
for all x.