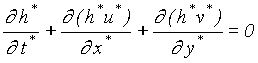 , (1a)
, (1a)Longshore Currents in the Swash Zone
Dang Van To*, Lecturer
Harumichi Kyotoh, Associate Professor
Water Engineering and Management Program, School of Civil Engineering
Asian Institute of Technology
P.O.Box 4 Klong Luang, Pathumthani 12120, Thailand
Tel : (66)-(2)-524-5558 - Fax: (66)-(2)-524-6059
Email : [email protected]
Abstract
A systematic approach in comparison with Ryrie’s (1983), which the multiple-scale perturbation technique is employed to nonlinear shallow water equations, so as to derive governing equations of first order for longshore currents in the swash zone, an alternately wet-dry region on the beach, is provided. In this study, the effect of the bottom unevenness to the currents under the obliquely incident waves with small incident angle is investigated. Analytically, a simple solution of the longshore currents can be obtained and its dependence on the bottom amplitude is indicated, by which cells or circulation stemming the longshore currents may be found if this bottom amplitude is large enough. In particular, assuming that the gradient of bottom topography along the shoreline is equal to zero, the particular first order solution of longshore current, v1p , now clearly satisfies the flat bottom surface condition as same as what has been done by Brocchini and Peregrine (1996). Interestingly, it may be found that the gravity effects in the swash zone and the surf zone are correspondingly different. It seems to be that the gravity force in the swash zone becomes stronger than one in the surf zone because of the very thin sheet of water.
Keywords : longshore currents, swash zone, perturbation method, shallow water equations.
1. INTRODUCTION
The swash zone with wave run-up and run-down on a beach forms the boundary between the surf zone and the backshore. It also determines the landward boundary of the area effected by wave actions where most of the coastal engineers, oceanographers, marine geologists recently are very much interested in, since a quantitative understanding of the swash zone hydrodynamics and sediment transport on beaches is essential for the design of coastal structures, shoreline erosion mitigation measures such as sand by passing and beach nourishment.
Evidently, the swash zone is closely related to human being activities, the existence of longshore currents causing particle zigzag motion in this uprush and backwash region therefore has been mentioned long ago by Zenkovich (1969) and Komar (1976). Recently, field and laboratory measurements on the distribution of longshore sediment transport across the surf zone indicated that the distribution was generally bimodal with peaks in the swash and breaker zone (see Kamphuis, 1991).
Surprisingly, while the longshore currents in the surf zone have been intensively investigated and developed by the concept of radiation stresses (Longuet-Higgins,1964), on the contrary, there are of definitely few studies on this problem in the swash zone except some of Asano (1994), Kobayashi (1994), Brocchini and Peregrine (1996). As a result, our knowledge in this region is equally restricted and challenging. This might be attributed not only to the difficulty for obtaining the radiation stresses in this alternately wet and dry region, but also the complexity and highly non linearity of the problem. The problem of longshore currents is considered under this motivation.
There are four sections in this study. Firstly, introduction is given in section 1, then in section 2 mathematical consideration using the nonlinear shallow water equation and derivation of analytical solution by multiple scale perturbation methods are provided, finally, discussions and conclusion are presented in section 3 and 4.
2. Mathematical Model
As for understanding the symbols in the model, some basic definitions are introduced by choosing the coordinate parallel to the bottom as x, y, still water level as z = 0 and t referring to time, while
h denotes the free surface displacement, h = d + h is the total water depth, d is the still water depth, R is run-up, u(x,y,t), v(x,y,t) are cross shore and longshore components of the depth average water velocity (see, Fig. 1).
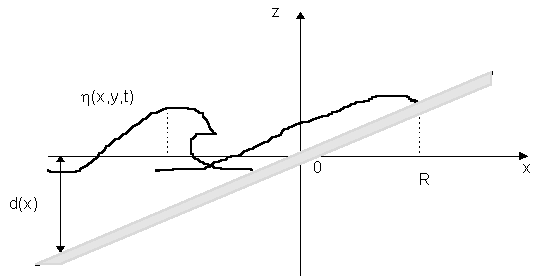
Figure 1. Surface definition in the vicinity of the swash zone
2.1. Governing Equations
The nonlinear shallow water equations are a good approximation to inviscid flow when any variations of surface level or mean velocity have a length-scale many times longer than the maximum depth of water. Such an approximation comes from the fact that both vorticity and vertical accelerations are assumed to be negligibly small.
In this study, assuming a beach of uniform slope
a , total water depth h(x,y,t) = - a x + h (x,y,t) + b(y), in which b(y) indicates the longshore direction of bottom unevenness topography, the dimensional governing equations for mass and momentum are written below
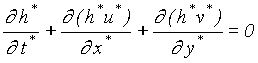 , (1a)
, (1a)
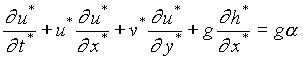 , (1b)
, (1b)
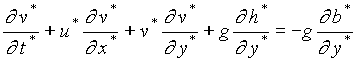 , (1c)
, (1c)
where superscript ‘*’ stands for dimensional quantities.
Dimensionless variables selected to eliminate the beach slope from equations (1a, b, c) are
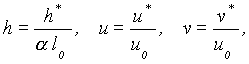 (2a)
(2a)
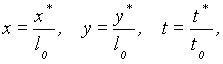 (2b)
(2b)
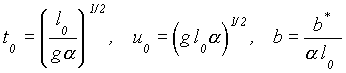 . (2c)
. (2c)
where l0 is a chosen reference depth, e.g. the depth of water at the certain seaward boundary. The equations (1a, b, c) then become
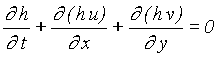 (3a)
(3a)
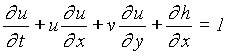 (3b)
(3b)
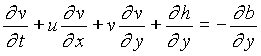 (3c)
(3c)
Equations (3a, b, c) are now served as the governing equations for the problem in this study. In addition, if waves approach the beach of small unevenness bottom by small incident angle, the mentioned equations can be further simplified.
2.2. Analytical Solution Using Perturbation Methods
On the basis of the foregoing assumptions, equations (3a, b, c) are solved analytically by the perturbation methods, a powerful tool for the approximate solutions of certain types of nonlinear problems, the expansion of solutions h, u, v in series with respect to
e are known as follows![]() ,
,
![]() ,
,
![]() . (4)
. (4)
It is necessary to introduce the multiple scales so that the elimination of secular terms can be made. Hence, independence variables (x,y,t) are now assumed to depend on (x, x1, x2 ...; y, y1, y2 ...; t, t1, t2 ...) , where
![]()
![]()
![]() (5)
(5)
and then treating these slow variables in a perturbation analysis as if they were independent. Here, bed surface level z = b is assumed to be a function of x1 and y1. Note that there is no dependence of variable y on the perturbation solution.
Substituting the perturbation expansions (4), slow variables (5) into equations (3a, b, c) and gathering together all the terms properly, the original nonlinear equations has been later reformulated into an infinite set of general form of the perturbed equations with ascending orders as
![]() (6)
(6)
The required condition that the quality holds for arbitrary e is that the efficient of like powers of e must be equal. Therefore,
![]() (7)
(7)
By this, the 0th-order perturbation equations corresponding to the normal incident waves of the one dimensional wave propagation are derived
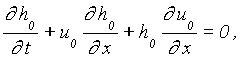 (8a)
(8a)
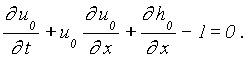 (8b)
(8b)
This one-dimensional problem was already studied intensively using the method of characteristics (Hibberd and Peregrine (1979)).
Similarly, the first order perturbation equations are given as
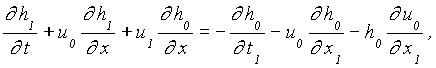 (9a)
(9a)
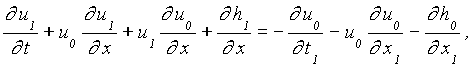 (9b)
(9b)
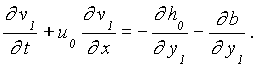 (9c)
(9c)
Obviously, these perturbation equations of first order yield decoupled equations each for on-offshore motion and for longshore motion, respectively. Accordingly, the longshore velocity v1(x,y,t) is easily solved like one-dimensional analysis once h(x,y,t), u(x,y,t), b(y) are known.
In physical terms, the decoupling of the on-shore and longshore momentum equation (9a, b, c) means that any effect on the onshore motion of interaction between on-shore and longshore motion is neglected. Moreover, the right hand side of equation (9a, b, c) implies the external forces, which can be determined by equations (8a, b) and the solvability of equations (9a, b, c). Ryrie (1983) stressed that the longshore velocity v1 could be determined without obtaining u1 and h1. In case of ![]() , the analytical solution of the alongshore velocity, v1, was found by Brocchini and Peregrine (1996) utilizing Carrier and Greenspand’s solution (1958).
, the analytical solution of the alongshore velocity, v1, was found by Brocchini and Peregrine (1996) utilizing Carrier and Greenspand’s solution (1958).
In our study, it is necessary to give the explicit functional form of h0 in terms of y1 so as to solve equations (9a, b, c). It is easy to suggest their form for the obliquely incident wave over the sinusoidal wavy bed surface as follow
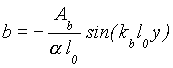 , (10)
, (10)
with new variables
![]() , (11a)
, (11a)
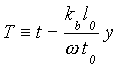 , (11b)
, (11b)
![]() . (11c)
. (11c)
Substituting equation (10) into (9c), then the external force becomes
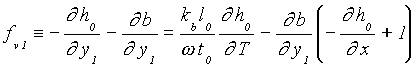 , (11b)
, (11b)
comparing the above formula with the 0-th order equation, the solution of equation (9c) is described by
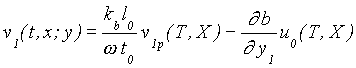 , (12)
, (12)
where v1p satisfies the subsequent flat-bottom equation
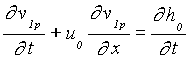 . (13)
. (13)
The second term in the right hand side of equation (12) is clearly indicating the effect of bottom unevenness
3. Discussion
Mathematically, our derivation of the perturbation equations is more systematic comparing to the former researchers. However, in order to obtain the explicit form of solution, knowledge of the previous studies are quite useful (see Ryrie (1983), Brochhini and Peregrine (1996)). In principle, the higher order of the perturbation equation might be easily obtained, but the inherent properties and phenomena must still be considered under much attempts. So far, although the first order of solution is accomplished by using the geometrical knowledge, higher order approximate solution needs systematic methods and physical background for further development.
Physically, It may be found that the gravity effect in the swash zone and the surf zone is quite different. In the surf zone, the longshore currents become very strong after wave-breaking, but the gravity force is negligibly small comparing to the other effects such as turbulent and dispersion. On the contrary, it is attributed to the very thin water sheet by run-up and run-down in the swash zone, the gravity effect clearly has a couple of contribution as seen in (12), for instant, the direction of longshore current can be changed under specific bottom topography. As a result, if the amplitude in (12) of the bottom is large enough, the longshore current in this area might be stemmed or flow into the opposite direction. Up to now, It is seemingly that the gravity force in the swash zone becomes stronger than in the surf zone because of the very thin sheet of water (sheet flow).
4. Conclusion
There is a very limited number of boundary value problems for which we can obtain exact solutions. Especially, for nonlinear shallow water equations, the solution is very difficult to achieve. However, by using multiple-scale perturbation method, the initial attempts to derive the first and second order of these equations are systematically made. Under certain assumptions, the perturbation equations in this study can be evidently as same as the previous published studies. For instant, in case the bottom unevenness is omitted, it results in a particular solution
v1p which clearly satisfies the flat bottom surface. A dependence of longshore current in the swash zone on the bottom unevenness is shown, by which the gravity effect in the swash zone and the surf zone is quite different. The gravity force in the swash zone becomes stronger than in the surf zone. For further development, higher order approximation would be required in association with the questionable phenomena to achieve a more systematic findings of longshore currents in the swash zone.References